| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] | [ Search: ] |
Written by Jorrit Tyberghein, jorrit.tyberghein@gmail.com.
Crystal Space supports three types of lighting: static, pseudo-dynamic and dynamic. They are different in the ways you can change their attributes while the engine is running. Static lights cannot be changed at all, but produce best performance and least memory consumption. Pseudo-dynamic lights can change their color and brightness, but not their position. Dynamic lights can also change their position.
In the interest of accuracy, it is actually possible to change the so-called “unchangeable” attributes of static and pseudo-dynamic lights, but after doing so, it is necessary to perform time-consuming recalculation of lightmaps in order for the changes to be reflected in the rendered world.
Every light has a position in world space coordinates and a current sector. Every light also has a radius (expressed in squared distance). This radius indicates where the light levels of the three light tables will reach zero.
This section gives a very brief explanation of the static lighting system used in Crystal Space. Warning: Although the basic principle described here is still valid, much more is going on now. This document needs to be updated to reflect the current state of the engine.
Static lighting is based on lightmaps. These are like textures except that every pixel defines the combined brightness of all lights at its position. Before the rendering loop starts, these lightmaps are precalculated so there is little performance loss at runtime, where we only need to blend texture and lightmap of a polygon.
Lightmaps are calculated as follows:
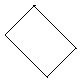
To create the three lightmaps for every polygon a 2D bounding box in texture space is calculated. This defines a rectangle that overlaps with the texture on the polygon and is correctly aligned with it (so that every 16 by 16 texel grid has one lightmap position). A consequence of this is that rotated textures can waste a lot of lightmap space. For example, see the following polygon:

And assume that the texture is aligned horizontally. Then we would need a lightmap of the following size:
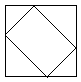
Note also, that the texture in the texture cache will have that size.
The pseudo-dynamic lighting system is an extension to the static lighting system described above. Pseudo-dynamic lights can not move but you can change the intensity or color. When some light is made pseudo-dynamic (a simple flag) the processing is a bit different. The shadow-computation remains the same but every polygon that is hit by the pseudo-dynamic light needs to have separate lightmaps for every pseudo-dynamic light that hits the polygon. So in the end all the polygons that are only hit by static lights have just one lightmap (for the three tables) for all static lighting information. Every polygon that is hit by one or more pseudo-dynamic lights will have one or more extra lightmap tables for every pseudo-dynamic light and one extra for all static lights. This information is then added together to result in the final lightmap table that can then be used by the texture cache routine (as explained earlier).
The lightmaps for the pseudo-dynamic lights are stored without the strength of the light. So where the light shines brightest the value in the lightmap will be 255, and where it shines least bright the value will be 0. When combining all pseudo-dynamic lightmaps and the static lightmap the strength of every light will be multiplied with the distance value to result in the real lightmap value. This also implies that there is only one extra lightmap for every polygon/pseudo-dynamic light because the shadow information (which is basically what is represented in pseudo-dynamic lightmaps) is the same for all three light-tables.
Here are some performance considerations for pseudo-dynamic lighting. There is a memory penalty for every polygon that is hit by some pseudo-dynamic lighting because extra lightmaps need to be created. So if you use no pseudo-dynamic lighting you will suffer no penalty but if you use a very large pseudo-dynamic light (with a large radius) it will probably hit a large number of polygons and you will have a considerable increase in memory requirements.
There is also a performance penalty whenever the intensity of a pseudo-dynamic light changes. This is because all the textures for the polygons that are hit by the pseudo-dynamic light need to be recalculated (they are removed from the texture cache).
If the intensity of a pseudo-dynamic light does not change there is no performance hit at all.
Crystal Space also supports true dynamic lights. These are rendered atop the normal lightmaps as explained above and support colors and limited shadows.
The algorithm to see if a given beam reaches a specific point on some polygon works as follows. The beam is described as two vertices (start and end):
A similar algorithm is used for Things.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
This document was generated using texi2html 1.76.